Расчет коэффициента вариации в Microsoft Excel

Одним из основных статистических показателей последовательности чисел является коэффициент вариации. Чтобы его найти, производятся довольно сложные расчеты. Инструменты Microsoft Excel значительно упрощают работу пользователя.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Результат выражается в процентах.

В Excel нет отдельной функции для расчета этого показателя, но есть формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, то есть они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его еще называют, стандартное отклонение, представляет собой квадратный корень из дисперсии. Функция СТАНДОТКЛОН используется для вычисления стандартного отклонения. Начиная с Excel 2010, он разделен, в зависимости от того, выполняется ли расчет по генеральной совокупности или по выборке, на два отдельных параметра: STDEV и STDV.

Синтаксис этих функций выглядит так:

= СТАНДОТКЛОН (Число1; Число2;…)
= СТАНДАРТНЫЙ (Число1; Число2;…)
= СТАНДОТКЛОН.V (Число1; Число2;…)

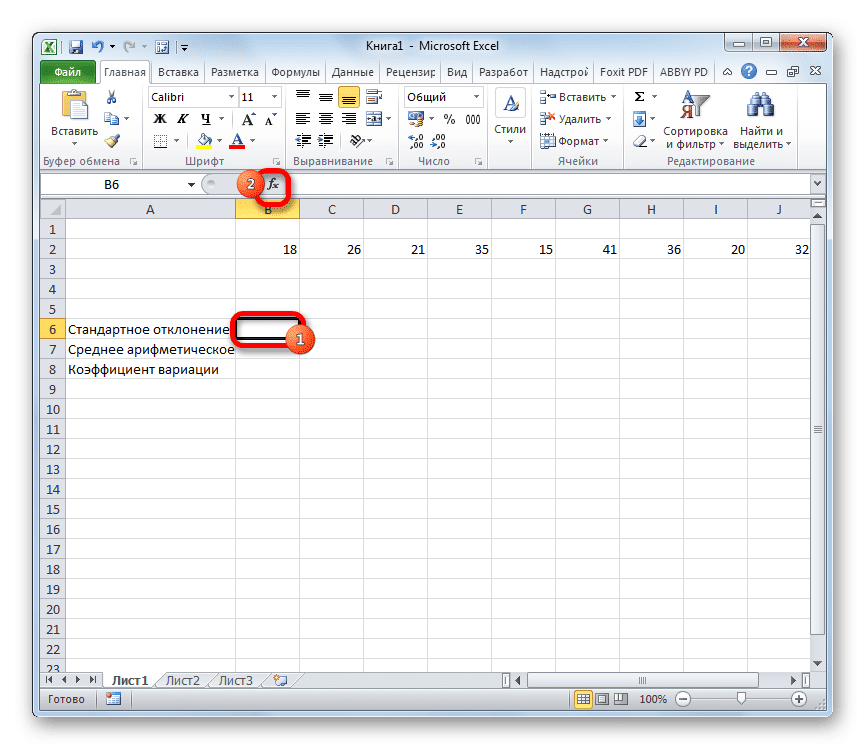
1. Для расчета стандартного отклонения выделите любую свободную ячейку на листе, удобную для вас, чтобы просмотреть в ней результаты расчета. Нажмите кнопку «Вставить функцию». Он выглядит как значок и находится слева от строки формул.
2. Мастер активируется, который запускается как отдельное окно со списком аргументов. Перейдем к категории «Статистика» или «Полный алфавитный список». Мы выбираем имя «СТАНДОТКЛОН.G» или «СТАНДОТКЛОН.V», в зависимости от того, будет ли расчет выполняться для генеральной совокупности или для выборки. Щелкните кнопку «ОК».
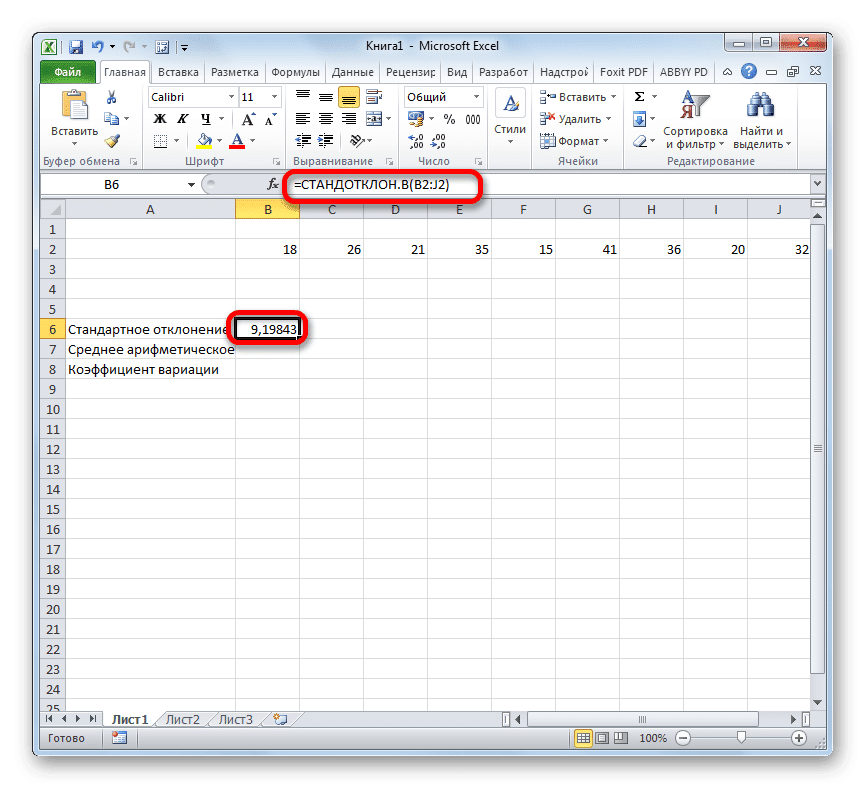
3. Откроется окно аргументов для этой функции. Он может иметь от 1 до 255 полей, которые могут содержать как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». С помощью мыши выберите диапазон значений, которые вы хотите обработать на листе. Если таких участков несколько и они не примыкают друг к другу, координаты следующей указываются в поле «Число 2» и так далее. После того, как вы ввели все необходимые данные, нажмите кнопку «ОК»
4. Итоговая сумма для выбранного типа стандартного отклонения отображается в предварительно выбранной ячейке.

Шаг 2: расчет среднего арифметического

Среднее арифметическое — это отношение общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя также есть отдельная функция — СРЕДНИЙ. Рассчитаем его значение на конкретном примере.

1. Выберите ячейку на листе, чтобы просмотреть результат. Нажмите на кнопку «Вставить функцию», с которой мы уже знакомы».
2. В статистической категории мастера найдите имя «СРЕДНИЙ». После выделения нажмите кнопку «ОК».
3. Откроется окно темы МЕДИА. Аргументы полностью идентичны аргументам групповых операторов STDEVP. То есть ими могут выступать как отдельные числовые значения, так и ссылки. Установите курсор в поле «Число 1». Как и в предыдущем случае, выделяем на листе нужный нам набор ячеек. После ввода их координат в поле окна темы нажмите кнопку «ОК».
4. Результат вычисления среднего арифметического отображается в ячейке, выбранной перед открытием мастера.

Шаг 3: нахождение коэффициента вариации

Теперь у нас есть все данные, необходимые для прямого расчета самого коэффициента вариации.

1. Выберите ячейку, в которой будет отображаться результат. Прежде всего необходимо учитывать, что коэффициент вариации — это процент. В связи с этим формат ячейки следует изменить на соответствующий. Сделать это можно, выбрав его, находясь во вкладке «Главная». Щелкните поле формата на ленте на панели инструментов «Число». В раскрывающемся списке параметров выберите «Процент». После этих действий формат элемента будет соответствующим.
2. Вернитесь в ячейку, чтобы увидеть результат. Активируем его двойным щелчком левой кнопки мыши. Мы ввели знак «=». Выберите элемент, в котором находится общий расчет стандартного отклонения. Нажмите кнопку «разделить» (/) на клавиатуре. Затем выберите ячейку, в которой находится среднее арифметическое данного числового ряда. Чтобы вычислить и отобразить значение, нажмите кнопку Enter на клавиатуре.
3. Как видите, результат расчета отображается на экране.

Затем мы выполнили расчет коэффициента вариации, обращаясь к ячейкам, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но вы можете действовать несколько иначе, не рассчитывая эти значения отдельно.

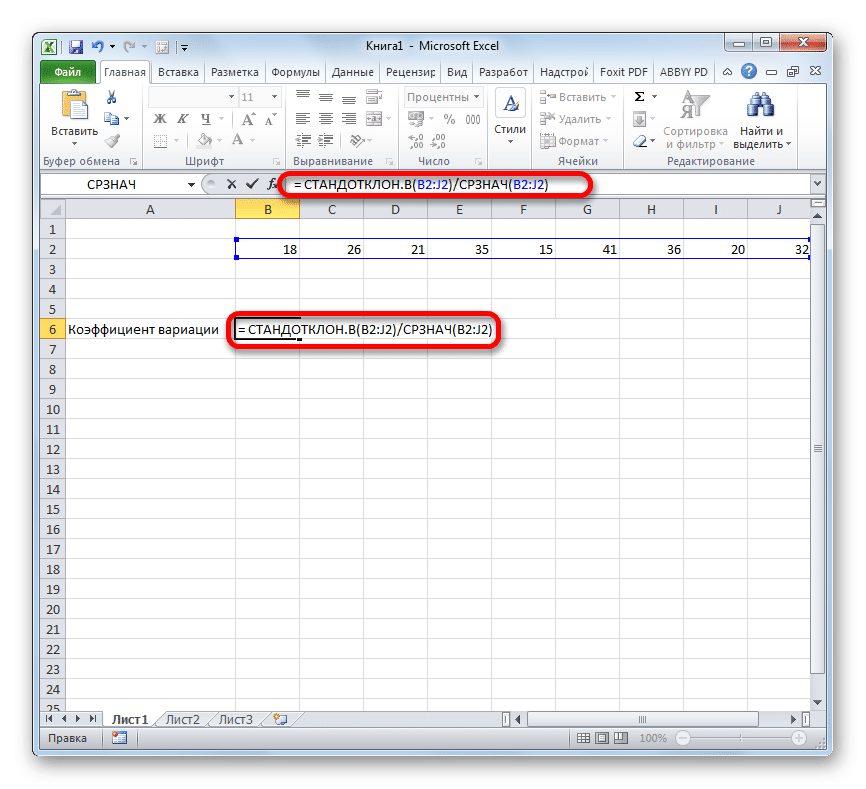
1. Выберите предварительно отформатированную ячейку для процентного формата, в которой будет отображаться результат. Запишем в него формулу вида:

   = СТАНДОТКЛОН.V (диапазон_значений) / СРЕДНИЙ (диапазон_значений)

   Вместо названия «Диапазон значений» вставляем реальные координаты области, в которой находится исследуемый числовой ряд. Это можно сделать, просто выделив этот диапазон. Вместо оператора STDEV.V, если пользователь сочтет это необходимым, можно использовать функцию STDEV.V.

2. Затем, чтобы рассчитать значение и отобразить результат на экране монитора, нажмите кнопку Enter.

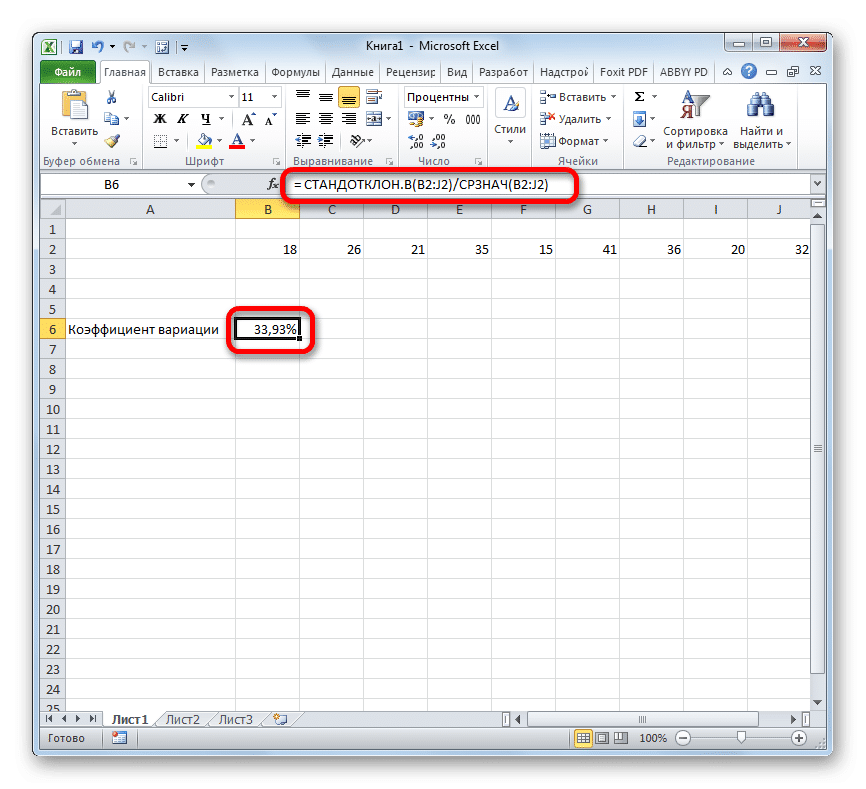
Есть условное различие. Считается, что если коэффициент вариации меньше 33%, набор чисел однороден. В противном случае его принято характеризовать как неоднородное.

Как видите, программа Excel позволяет значительно упростить расчет такого сложного статистического расчета, как поиск коэффициента вариации. К сожалению, в приложении пока нет функции, вычисляющей этот показатель за одно действие, но с помощью операторов STDEV и AVERAGE эта задача значительно упрощается. Поэтому даже человек, не обладающий высокими знаниями в области статистических законов, может сделать это в Excel.