Функция REPLACE заменяет старый текст новым текстом в текстовой строке. Функция заменит все повторы старого текста, пока не будет выполнено определенное условие. Это чувствительно к регистру.
Как можно использовать функцию SUBSTITUTE (ПОДСТАВИТЬ)?
Функция REPLACE заменяет старый текст новым текстом в текстовой строке. Вы можете использовать его для:
- Измените название региона в заголовке отчета.
- Удалите непечатаемые символы.
- Заменить последний пробел.
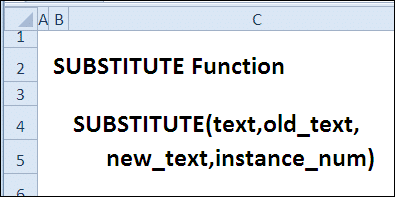
Синтаксис SUBSTITUTE (ПОДСТАВИТЬ)
Функция REPLACE имеет следующий синтаксис:
ЗАМЕНИТЬ (текст; старый_текст; новый_текст; номер_экземпляра)
ЗАМЕНИТЬ (текст; старый_текст; новый_текст; номер_входа)
- текст (текст) — текстовая строка или ссылка, в которой будет заменен текст.
- old_text (old_text) — текст, который нужно заменить.
- new_text (новый_текст) — текст для вставки.
- instance_number (instance_number) — номер вхождения заменяемого текста (необязательно).
Замена или удаление неразрывных пробелов
При загрузке данных из 1С, копировании информации с веб-страниц или документов Word часто приходится иметь дело с неразрывным пробелом: специальным символом, неотличимым от обычного пробела, но с другим внутренним кодом (160 вместо 32). Его нельзя удалить стандартными средствами, заменив его с помощью диалогового окна Ctrl + H или с помощью функции TRIM для удаления лишних пробелов. Наша функция REPLACE поможет вам, с помощью которой вы можете заменить неразрывный пробел простой или пустой текстовой строкой, например Удалить:
Формула = ПОИСКПОЗ («ПЕРВЫЙ»; «Первый») вернет ЛОЖЬ, например. 2 текстовых значения не соответствуют РЕГИСТРАЦИИ. Formula = EXACT («ПЕРВЫЙ»; «ПЕРВЫЙ») вернет ИСТИНА.
Допустим, в ячейку A2 вставлена строка First channel — лучшее, а в ячейке A3 — строка FIRST channel — лучшее. Для сравнения строк с учетом РЕГИСТРАЦИИ используйте формулу = ТОЧНО (A2; A3), для сравнения значений без ЗАПИСИ используйте формулу = A2 = A3 .
Выборочная дисперсия (выборочная дисперсия) характеризует разброс значений в массиве относительно среднего .
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что дисперсия выборки — это сумма квадратов отклонений каждого значения в массиве от среднего, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях функция VAR () используется для вычисления выборочной дисперсии. Имя VAR, например Дисперсия. Начиная с версии MS EXCEL 2010 рекомендуется использовать его аналог DISP.B () с именем VARS, т.е дисперсия выборки. Кроме того, начиная с версии MS EXCEL 2010 существует функция DISP.G (), английское название VARP, то есть POPULATION VARIANCE, которая вычисляет дисперсию для всей генеральной совокупности. Вся разница сводится к знаменателю: вместо n-1, как в DISP.B (), DISP.G () имеет только n в знаменателе. До MS EXCEL 2010 функция VARP () использовалась для вычисления дисперсии генеральной совокупности() .
Дисперсия выборки также может быть рассчитана напрямую с помощью следующих формул (см. Файл примера) = SQD (образец) / (COUNT (Sample) -1) = (SUMS (Sample) -COUNT (Sample) * AVERAGE (Sample) ^ 2) / (COUNT (Sample) -1) — обычная формула = SUM ((Sample-AVERAGE (Sample)) ^ 2) / (COUNT (Sample) -1) — матричная формула
Дисперсия выборки равна 0, только если все значения равны друг другу и, следовательно, равны среднему значению. Как правило, чем больше дисперсия, тем больше разброс значений в массиве.
Дисперсия выборки — это точечная оценка дисперсии распределения случайной величины, из которой была взята выборка. О построении доверительных интервалов при оценке дисперсии вы можете прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .
Чтобы вычислить дисперсию случайной величины, вам необходимо знать ее функцию распределения .
Для дисперсии случайной величины X часто используется обозначение Var (X). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E (X): Var (X) = E [(XE (X)) 2]
Если случайная величина имеет дискретное распределение, дисперсия рассчитывается по формуле:
где xi — значение, которое может принимать случайная величина, а μ — среднее значение (математическое ожидание случайной величины), p (x) — вероятность того, что случайная величина примет значение x.
Если случайная величина имеет непрерывное распределение, дисперсия рассчитывается по формуле:
где p (x) — плотность вероятности .
Для распределений, представленных в MS EXCEL, дисперсию можно рассчитать аналитически как функцию параметров распределения. Например, для биномиального распределения дисперсия равна произведению его параметров: n * p * q.
Примечание: дисперсия, которая является вторым центральным моментом, обозначается D [X], VAR (x), V (x). Второй центральный момент — это числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .
Примечание: Вы можете прочитать о распределениях в MS EXCEL в статье Распределения случайной переменной в MS EXCEL .
Размер отклонения — квадрат единицы измерения исходных значений. Например, если значения в выборке являются измерениями веса детали (в кг), размер отклонения будет 2 кг. Это может быть трудно интерпретировать, поэтому для характеристики разброса значений, они часто используют значение, равное квадратному корню из дисперсии — стандартному отклонению .
Некоторые дисперсионные свойства :
Var (X + a) = Var (X), где X — случайная величина, а a — константа.
Var (aX) = a 2 Var (X)
Var (X) = E [(XE (X)) 2] = E [X 2 -2 * X * E (X) + (E (X)) 2] = E (X 2) -E (2 * X * E (X)) + (E (X)) 2 = E (X 2) -2 * E (X) * E (X) + (E (X)) 2 = E (X 2) — (E (Х)) 2
Это свойство дисперсии используется в статье о линейной регрессии .
Var (X + Y) = Var (X) + Var (Y) + 2 * Cov (X; Y), где X и Y — случайные величины, Cov (X; Y) — ковариация этих случайных величин.
Если случайные величины независимы, их ковариация равна 0 и, следовательно, Var (X + Y) = Var (X) + Var (Y). Это свойство дисперсии используется для получения стандартной ошибки среднего .
Докажем, что для независимых величин Var (XY) = Var (X + Y). Действительно, Var (XY) = Var (XY) = Var (X + (- Y)) = Var (X) + Var (-Y) = Var (X) + Var (-Y) = Var (X) + (- 1) 2 Var (Y) = Var (X) + Var (Y) = Var (X + Y). Это свойство дисперсии используется для построения доверительного интервала для разницы двух средних .
Стандартное отклонение выборки — это мера того, насколько широко значения распределены в выборке по отношению к их среднему значению .
По определению стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение не учитывает величину значений в выборке, а только степень разброса значений вокруг их среднего значения. Вот пример, чтобы проиллюстрировать это.
Мы рассчитываем стандартное отклонение для 2 образцов: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях s = 4. Очевидно, что соотношение между стандартным отклонением и значениями массива существенно различается для выборок. Для таких случаев используется коэффициент вариации (CV) — отношение стандартного отклонения к среднему арифметическому, выраженное в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления стандартного отклонения выборки используется функция = СТАНДОТКЛОН () имя СТАНДОТКЛОН, т.е стандартное отклонение. Начиная с версии MS EXCEL 2010 рекомендуется использовать его аналог = STDEV () с именем STDEV, т.е пример стандартного отклонения.
Кроме того, начиная с версии MS EXCEL 2010 существует функция СТАНДОТКЛОН () с именем СТАНДОТКЛОН, т.е стандартное отклонение совокупности, которая вычисляет стандартное отклонение для совокупности. Вся разница сводится к знаменателю: вместо n-1 как STDEV (), STDEV () имеет только n в знаменателе.
Стандартное отклонение также можно рассчитать напрямую, используя следующие формулы (см. Файл примера) = ROOT (КВАДРАТ (образец) / (COUNT (Sample) -1)) = ROOT ((SUM (Sample) -COUNT (Sample) * AVERAGE) (Образец)) ^ 2) / (СЧЁТ (Образец) -1))
Пример 1. В компании два менеджера по привлечению клиентов. Данные о количестве клиентов, обслуживаемых ежедневно каждым оператором, заносятся в таблицу Excel. Определите, кто из двух сотрудников работает лучше.
Таблица исходных данных:
Для начала посчитаем среднее количество клиентов, с которыми менеджеры работали ежедневно:
= СРЕДНИЙ (B2: B11)
Эта функция вычисляет среднее арифметическое для диапазона B2: B11, который содержит данные о количестве клиентов, ежедневно получаемых первым менеджером. Аналогично рассчитываем среднее количество клиентов в день для второго менеджера. У нас есть:
Судя по полученным значениям, оба менеджера работают примерно одинаково. Однако визуально можно увидеть сильный разброс количества клиентов премьер-менеджера. Мы рассчитываем стандартное отклонение по формуле:
= СТАНДОТКЛОН.B (B2: B11)
B2: B11 — диапазон исследуемых значений. Аналогичным образом определяем стандартное отклонение для второго менеджера и получаем следующие результаты:
Как видите, показатели эффективности первого руководителя характеризуются большой вариабельностью (разбросом) значений, поэтому среднее арифметическое значение совершенно не отражает реальной картины эффективности работы. Отклонение 1,2 свидетельствует о более стабильной и, следовательно, более эффективной работе второго руководителя.
Пример 2. Две разные группы студентов университета были протестированы по одной и той же дисциплине. Оцените успеваемость ученика.
Таблица исходных данных:
Определите стандартное отклонение значений для первой группы по формуле:
= СТАНДОТКЛОН (A2: A11)
Аналогичный расчет проделаем для второй группы. В результате получаем:
Полученные значения свидетельствуют о том, что студенты второй группы подготовились к экзамену намного лучше, поскольку разброс оценок относительно невелик. Обратите внимание, что функция СТАНДОТКЛОН преобразует текстовое значение «сбой» в числовое значение 0 (ноль) и учитывает это в расчетах.
Вставьте строку Продажи (январь) в ячейку A2. Чтобы заменить слово январь на февраль, напишем формулы:
= REPLACE (A2; 10; 6, «Февраль») = REPLACE (A2, «Январь», «Февраль”)
те функции REPLACE (), которые необходимы для вычисления начальной позиции слова Январь (10) и его длины (6). Это неудобно, функция ПОДСТАВИТЬ () намного проще справляется с задачей.
Кроме того, функция REPLACE () заменяет, по очевидным причинам, только одно вхождение строки, функция SUBSTITUTE () может заменять все вхождения или только первое, только второе и т.д. Давайте объясним это на примере. Вставьте строку Продажи (январь), Прибыль (январь) в ячейку A2. Записываем формулы: = REPLACE (A2; 10; 6; «Февраль») = REPLACE (A2; «Январь»; «Февраль») получаем в первом случае строку Продажи (февраль), прибыль (январь), в второй — Продажи (февраль), прибыль (февраль). Записывая формулу = ПОДСТАВИТЬ (A2; «Январь»; «Февраль»; 2) получаем строку Продажи (январь), прибыль (февраль) .
Кроме того, функция SUBSTITUTE () может быть чувствительной к регистру, а функция REPLACE (), по очевидным причинам, не может.
Возвращает текстовую строку, в которой старый текст был заменен новым.
- текст (текст) — текст, который нужно заменить;
- old_text (old_text) — старый текст, в котором будет происходить замена;
- new_text (новый_текст) — новый текст для замены;
- [instance_number] (необязательно) — определяет, какой экземпляр текста будет заменен. Если аргумент не указан, замена будет производиться по всему тексту.
Пример 1. После вычислений, выполненных в конкретном приложении, были получены некоторые значения, записанные в таблицу Excel. Некоторые значения не могли быть вычислены, и вместо числового представления была сгенерирована ошибка «NaN». Вы должны заменить все значения «NaN» на число 0 в соответствующих строках.
Таблица данных:
Для подстановки и подстановки мы используем формулу, рассматриваемую как массив. Сначала выберите диапазон ячеек C2: C9, затем введите формулу с помощью комбинации Ctrl + Shift + Enter:
Функция VALUE преобразует полученные текстовые строки в числовые значения. Описание аргументов функции ЗАМЕНИТЬ:
- B2: B9 — диапазон ячеек, в котором нужно заменить часть строки;
- «NaN» — заменяемая часть текста;
- 0 — фрагмент, который будет вставлен на место заменяемого фрагмента.
Чтобы заменить значения во всех ячейках, нажмите Ctrl + Shift + Enter, чтобы выполнить функцию в массиве. Результат расчета:
Точно так же функция заменяет значения другой таблицы при определенных условиях.
Пример 2. Домашний интернет-провайдер хранит данные о своих подписчиках в электронной таблице Excel. Допустим, Садовую улицу переименовали в Никольскую. Вам нужно быстро изменить название улицы в адресной строке каждого клиента.
Таблица данных:
Для выполнения данного условия воспользуемся формулой:
Примечание. В этом примере SUBSTITUTE также используется в массиве Ctrl + Shift + Enter.
