Мода в статистике

В статистике есть целый набор показателей, характеризующих центральный тренд. Выбор того или иного показателя зависит в основном от характера данных, цели расчетов и их свойств.
Что такое характер данных
Что подразумевается под характером данных? В первую очередь поговорим о количественных данных, которые выражаются цифрами. Но набор числовых данных может иметь разное распределение. Распределение относится к частотам отдельных значений. Например, в классе из 23 человек 2 ученика написали тест на двоих, 5 на троих, 10 на четыре и 6 на A. Это распределение оценок. Распределение можно очень наглядно представить с помощью специального графика — гистограммы. В этом примере вы получите следующую гистограмму.

Во многих случаях количество уникальных значений намного больше, и распределение кажется нормальным. Ниже представлена грубая иллюстрация нормального распределения случайных чисел.

Отсюда центральная тенденция. Если частоты анализируемых величин распределены по нормальному закону, то есть симметрично относительно определенного центра, центральная тенденция определяется достаточно однозначно: это сам центр и математически соответствует среднему арифметическому.
Как легко видеть, максимальная частота значений также находится в том же центре. То есть при нормальном распределении центральным трендом является не только среднее арифметическое, но и максимальная частота, которая в статистике называется режимом или модальным значением.
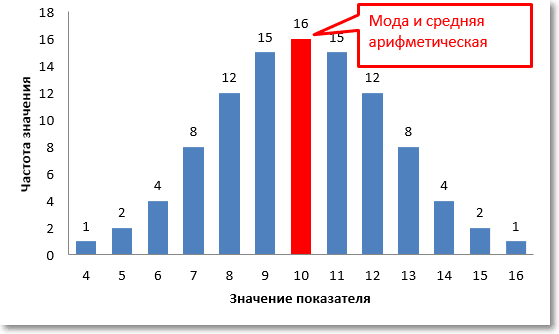
На диаграмме оба значения центрального тренда совпадают и равны 10.
Но такое распределение встречается далеко не всегда и при небольшом количестве данных встречается очень редко. Часто бывает, что частоты распределяются несимметрично. Тогда режим и среднее арифметическое не совпадут.

На рисунке выше среднее арифметическое все еще равно 10, но в моде уже 9. Что в данном случае считается значением центрального тренда? Ответ зависит от целей анализа. Если вас интересует уровень, сумма отклонений которого равна нулю со всеми вытекающими свойствами и последствиями, то это среднее арифметическое. Если вам нужно более частое значение, то это мод.
Так зачем тебе мод? Вот пара примеров. Экономист из отдела экономического планирования обувной фабрики спрашивает, какой размер обуви наиболее популярен. Средний размер обуви здесь, скорее всего, не подойдет, тем более, что число может оказаться дробным. Но мода — верный индикатор.
Расчет моды
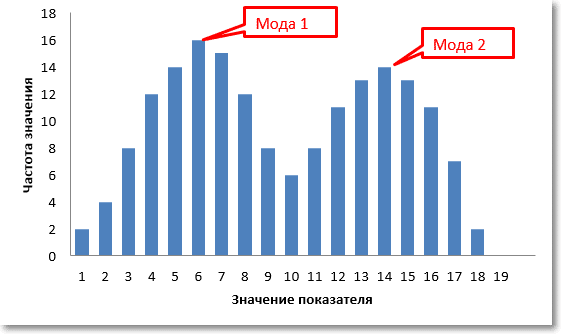
Посмотрим теперь, как рассчитать моду. Режим — это значение в анализируемом наборе данных, которое встречается чаще, чем другие, поэтому вам нужно посмотреть на частоту значений и найти максимум. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 режим будет 3 — он повторяется чаще других. Это сдержанная линия и здесь все просто. Если данных много, режим легче найти с помощью соответствующей гистограммы. Так получилось, что набор данных имеет бимодальное распределение.

Без диаграммы очень сложно понять, что в данных есть не один, а два центра. Например, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Следовательно, распределение доли голосов за данного кандидата может быть «двухсторонним». Первый «горб» — выбор городского населения, второй — сельского.
с данными диапазона немного сложнее, когда есть диапазоны вместо конкретных значений. В этом случае мы говорим о модальном интервале (например, при анализе доходов населения), то есть интервале, частота которого максимальна по сравнению с другими интервалами. Однако даже здесь можно найти конкретное модальное значение, даже если оно будет условным и приблизительным, так как точных исходных данных нет. Представьте, что у вас есть следующая таблица распределения цен.

Для наглядности изобразим соответствующую схему.

Во-первых, вам нужно определить модальный диапазон, который соответствует диапазону с самой высокой частотой. Найти его так же просто, как найти моду в сдержанной серии. В нашем примере это третий диапазон с ценой от 301 до 400 рублей. Самый высокий столбец на графике. Теперь необходимо определить конкретное значение цены, соответствующее максимальному количеству. Сделать это точно и по сути невозможно, так как нет индивидуальных значений частоты для каждой цены. Поэтому предполагается, что интервалы выше и ниже модального, в зависимости от их частоты, имеют разные веса и как бы толкают режим в своем направлении. Если частота интервала, следующего за модальным, больше, чем частота интервала перед модальным, то режим будет справа от центра модального интервала и наоборот. Давайте еще раз посмотрим на изображение, чтобы понять формулу, которую я запишу ниже.

На рисунке ясно видно, что соотношение между высотами столбцов, расположенных слева и справа от модального окна, определяет, насколько близко режим находится к левому или правому краю модального диапазона. Задача расчета модального значения — найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями), и найти соответствующее значение для характеристики (в нашем примере цена) . Зная азы геометрии (7 класс), из этого рисунка легко вывести формулу для расчета режима в серии интервалов.
Формула моды следующая.

Где Мо в моде
x0 — значение начала модального интервала,
h — размер модального интервала,
fМо — частота модального диапазона,
fМо-1 — частота интервала, предшествующего модальному,
fМо1 — частота интервала после модального.
Второй член в модальной формуле соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.

Следовательно, режим серии интервалов представляет собой сумму, составленную из значения начального уровня модального интервала и сегмента, который определяется соотношением частот интервалов, ближайших к модальному.
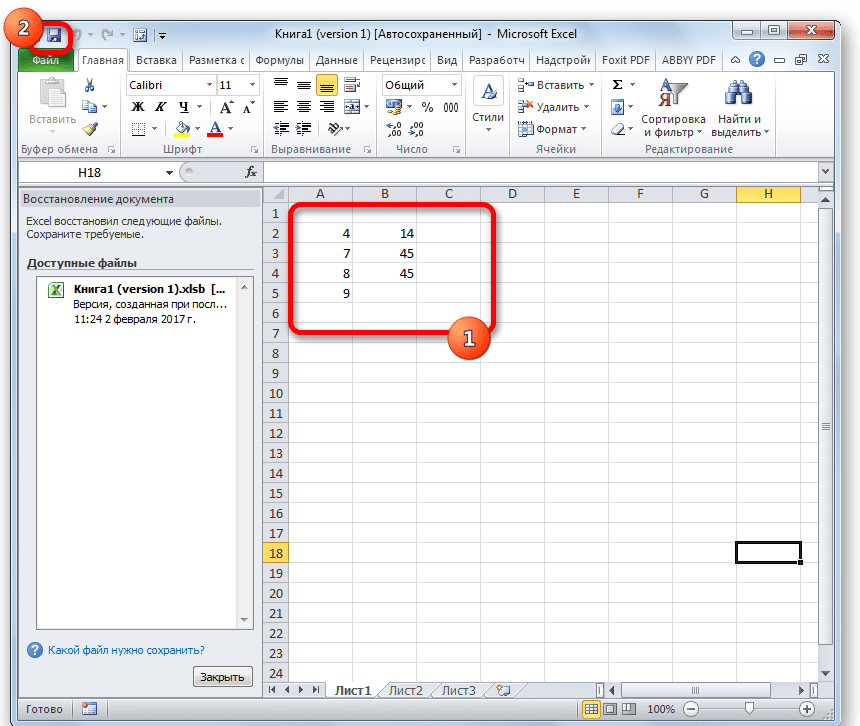
Расчет моды в Excel
В настоящее время большая часть расчетов выполняется в MS Excel, где также есть специальная функция для расчета режима. В Excel 2013 я нашел 3.

МОДА — это наследие старых редакций Excel. Функция оставлена для обратной совместимости.
FASHION.One — рассчитывает режим по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».
MODA.NSK — позволяет одновременно рассчитывать несколько модальных значений (одинаковые максимальные частоты) для ряда данных, если таковые имеются. Перед выбором количества ячеек, равного количеству требуемых модальных значений, функцию необходимо ввести как формулу массива. Иногда действительно модальных значений может быть несколько. Однако для этих целей лучше всего сначала взглянуть на диаграмму распределения.
Режим для данных диапазона не может быть рассчитан с помощью одной функции в Excel. То есть такая функция не предоставляется. Придется прописывать вручную.